Plant Calculator
How Many Plants Do You Need?
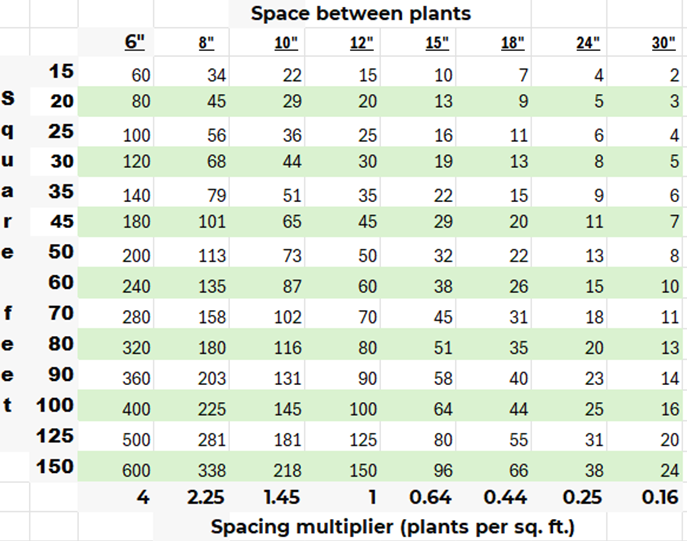
Above chart is for Grid planting method. For other sizes, shaped areas, and methods, see below and use the following formula to calculate how many plants you will need:
(Area in sq. feet) x (Spacing Multiplier) = Number of plants needed
(Area is 2 feet by 25 feet = 50 sq. feet) x (Spacing 12 inches apart Spacing Multiplier is 1.0 ) = 50 is the number of plants needed
Finding Unknown Spacing Multiplier
For other spacing requirements, use the following formula to figure your multiplier:
Multiplier = 144/X2 where X = the spacing distance in inches you need
Example: If you need a spacing of 13.5 inches, your plant multiplier would be 0.79:
|
144 |
= |
144 |
= |
0.79 |
13.52
|
182.25 |
multiplier |
The above chart and formula are based on planting in a grid pattern. If you are planting in a staggered or equilateral triangular pattern (which gives a more massed effect) the rows will be a little closer together and more plants will be needed.
An additional 15% will be required and the row spacing would be reduce by a factor of 0.866 (the sine of 60 degrees) for the equilateral triangular layout.
For example - based on 100 square feet and a spacing of 12 inches, 100 plants are needed. In a triangular pattern 15 more plants would be needed (100 x 15% = 15). Instead of 12-inch rows, rows would be 10.4 inches apart (12 x .866 = 10.392).
Grid vs. Triangular spacing
A grid spacing of plants is divided into areas of equal space and one plant in each center. Grid spacing allows for more area open space and has potential benefit for disease management, but it is not as space efficient as triangular spacing.
Triangular spacing, is a lattice of equilateral triangles (they all have sides of the same length, and all internal angles are equal to 60 degrees) with a plant in each corner. This arrangement maximizes the use of space but may increase the chance of spreading diseases. Triangular spacing is frequently used in landscaping.
Calculating for a circular planting area?
1. Determine the area of the circle:
- Measure the radius of the circle (distance from the center to any edge).
- Multiply the radius by itself and then by pi (3.14159). This gives you the area of the circle in square units.
2. Choose the desired plant spacing:
- Refer to the planting recommendations for your chosen plant species. This will typically specify the recommended spacing between individual plants to ensure optimal growth and density.
3. Divide the circle area by the plant spacing:
- Divide the total area of the circle (calculated in step 1) by the desired plant spacing (obtained in step 2). This gives you the approximate number of plants needed to fill the circle.
Here is an example:
- You have a circular planting area with a radius of 5 feet.
- You want to plant with a recommended spacing of 12 inches (1 foot).
Calculation:
- Area of the circle = 3.14 * 5^2 = 78.5 square feet
- Number of plants = 78.5 square feet / 1 square foot/plant = 78.5 plants
Note:
- Round the final number of plants up to the nearest whole number to ensure adequate coverage.
- Consider additional factors like plant growth habit and mature size when determining the final number of plants. You might need to adjust the spacing slightly to accommodate larger plants.